Outflow Parameters
June 22, 2017
The Chevalier & Clegg outflow model is characterized by just three parameters: the starburst radius, \(R_*\), the mass injection rate, \(\dot{M}\), and the energy injection rate, \(\dot{E}\). These parameters can be set for a given star formation rate by specifying how the total mass and energy injection compare to the rates that would be expected from the products of stellar evolution. In previous posts, I’ve used the term \(\beta\) to indicate the multiplicative factor that accounts for mass in the hot outflow that is not a product of supernovae and stellar winds, i.e. \(\dot{M}_\mathrm{hot} = \beta_\mathrm{hot} \dot{M}_\mathrm{SN+SW}\) - this is the usage that appears in Strickland and Heckman (2009). However, by selecting an IMF and making some (reasonable) assumptions about stellar evolution, this \(\beta_\mathrm{hot}\) can be converted into a different definition of mass loading, i.e. \(\dot{M}_\mathrm{hot} = \beta_\mathrm{SFR} \dot{M}_\mathrm{SFR}\). In this version, \(\beta_\mathrm{SFR}\) tells us how the total mass in the hot outflow compares to the star formation rate in the galaxy. A wind that has zero mass-loading (and therefore only contains mass from the byproducts of stellar evolution) would have \(\beta_\mathrm{hot} = 1\) and \(\beta_\mathrm{SFR} \sim0.25\) (see discussion in Section 2.1.1 of Veilleux et al. 2005 or results from Starburst 99 models in Leitherer 1999). The same calculation yields an estimate of the energy injected by supernovae and stellar winds as a function of star formation rate, with a typical number of \(\dot{E}_\mathrm{SN} = 3.0\times10^{41}\) erg \(\mathrm{s}^{-1}\) \(\alpha \dot{M}_\mathrm{SFR}\), where the factor \(\alpha\) accounts for the fraction of the energy that is thermalized in the hot plasma (see Section 2.1 of Thompson et al. 2016).
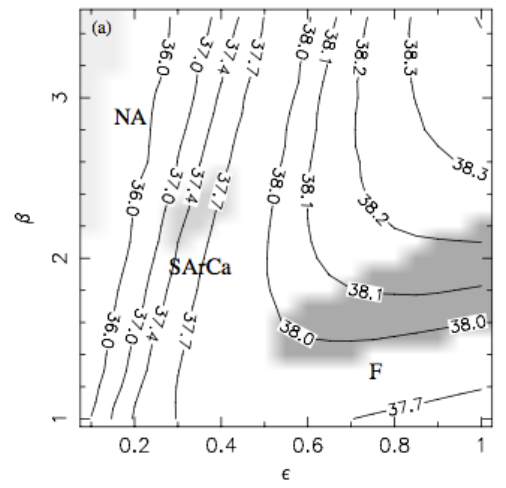
Using \(\beta_\mathrm{hot}\), Strickland & Heckman (2009) estimated values of both \(\alpha\) and \(\beta\). Using a model that assumes a continuous star formation rate of \(\dot{M}_\mathrm{SFR} = 4.7 M_\odot/\mathrm{yr}\) for 30 Myr, they find that \(\alpha\) ranges from 0.4 to 1.0 and \(\beta\) from 1.2 to 2.3, in models that match all observational constraints (the grey region marked ‘F’ in the figure reproduced below). Other parameters of their model include \(R_* = 300\) pc, \(Z_\mathrm{SN+SW} = 5 Z_\odot\), and \(Z_\mathrm{cold} = 1 Z_\odot\). These parameters yield \(\dot{E}_\mathrm{SN+SW} = 3.1\times10^{42}\) erg/s and \(\dot{M}_\mathrm{SN+SW} = 1.4 M_\odot\)/yr. \(\alpha\) and \(\beta\) have correlated values, as can be seen in the figure. If we convert \(\beta_\mathrm{hot}\) to \(\beta_\mathrm{SFR}\), we find that \(\beta_{SFR}\) ranges between 0.36 and 0.7.
What does this mean for the properties of a cooling outflow in M82? Using Equation 6 from Thompson et al. (2016), I can estimate the radius at which M82’s wind should cool, given specific values of \(\alpha\), \(\beta\), \(R_*\), and SFR. The equation reads \(r_\mathrm{cool} \simeq 4\mathrm{kpc}\frac{\alpha^{2.13}}{\beta^{2.92}}R_{0.3}^{1.79}\left(\frac{\Omega_{4\pi}}{\dot{M}_\mathrm{SFR, 10}}\right)^{0.789},\) where the subscript on \(R\) refers to a starburst radius in units of \(0.3\) kpc, and on \(\dot{M}\) refers to a star formation rate in units of 10 \(M_\odot\)/yr. If we plug in 0.9 for \(\alpha\), 4.7 for \(\dot{M}\) and 0.42 for \(\beta\) (the values used in the simulations shown in the last post), we get \(r_\mathrm{cool}\) = 73 kpc, well beyond the maximum radius allowed by subsequent equations in Thompson et al. (2016). If I leave the fiducial star formation rate at 10, I get \(r_\mathrm{cool}\) = 40 kpc, if I then lower \(\alpha\) to 0.5 and raise \(\beta\) to 0.5, I can get \(r_\mathrm{cool}\) down to 6.9 kpc - but this doesn’t make a lot of sense, given that \(\alpha\) and \(\beta\) are correlated. Changing the opening angle helps a bit - if we decrease it to 60 degrees, \(r_\mathrm{cool}\) with my fiducial parameters gives 24 kpc, and decreasing it to 30 degrees give 8.7 kpc. Based on the temperature slices of the simulation I ran, the opening angle for the hot outflow does look to be closer to 60 degrees than 180… but the simulation data along the z-axis also perfectly matches the Chevalier & Clegg analytic solution, which assumes a spherical outflow.