More outflow models
June 15, 2017
Recall that in the last post, I tested two outflow models. For a \(256^3\) simulation, when I used \(R_{*} = 200\)pc, \(\dot{M}_{\odot} = 1 M_{\odot}\)/yr, and \(\dot{E} = 10^{43}\)erg/s (aka CC85 parameters), I was able to generate an outflow, though the simulation crashed after 327 Myr. When I used \(R_{*} = 300\)pc, \(\dot{M}_{\odot} = 2 M_{\odot}\)/yr, and \(\dot{E} = 10^{42}\)erg/s (aka SR17 parameters), no outflow was generated, just a bubble of warm gas near the center.
In this post, I compare a variety of different parameter combinations to see when I’m able to drive an outflow. Below I summarize all the models and the results:
- Model 1: constant SR17 parameters; resolution \(128^3\); outflow
- Model 2: constant SR17 parameters; resolution \(256^3\); no outflow
- Model 3: constant CC85 parameters; resolution \(256^3\); strong outflow; crashes at 327 Myr
- Model 4: ramp up from SR17 to CC85 parameters over 25 Myr, stay at CC85 parameters for 25Myr, ramp back down to SR17 for the remainder of the simulation; resolution \(256^3\); no outflow
- Model 5: constant feedback in between SR17 and CC85, \(R_{*} = 300\)pc, \(\dot{M}_{\odot} = 2.5 M_{\odot}\)/yr, and \(\dot{E} = 0.8\times3.25\times10^{42}\)erg/s (corresponds to \(\beta = 1.6\), \(\epsilon = 0.8\) in Strickland & Heckman 2009); resolution \(256^3\); weak outflow, doesn’t escape box
- Model 6: ramp feedback from \(R_{*} = 300\)pc, \(\dot{M}_{\odot} = 2 M_{\odot}\)/yr, and \(\dot{E} = 0.8\times3.25\times10^{42}\)erg/s (\(\beta = 1.4\), \(\epsilon = 0.8\) in Strickland & Heckman 2009) to CC85 parameters, ramp up for 10 Myr, high for 30 Myr, ramp down for 10 Myr; weak outflow; crashes at 234 Myr
- Model 7: same as model 6 but with \(512^3\) resolution; no outflow
I won’t put movies of all the models up, but here are a couple that are representative (the first three models can be seen in the last post).
Model 5, temperature projection:
At this point, two things are becoming obvious. First, models that succeed in driving outflows also tend to crash. The crashes always happen in the halo, generally where outflowing gas is mixing with halo gas. This isn’t that surprising, since we’re dealing with large density / temperature gradients and high velocities and mach numbers. All of these simulations are producing negative temperatures at times. I’m currently running a dual-energy version of Model 3 to see if that fixes the problem.
The second issue is that as the resolution is increased, creating an outflow is getting more difficult. This one I need to unpack a little. Looking at the temperature slices, the reason I’m not getting outflows is fairly obvious - at higher resolution, I don’t generate high temperature gas. For example, compare these two temperature slices from Model 6 and Model 7.
Resolution \(256^3\):
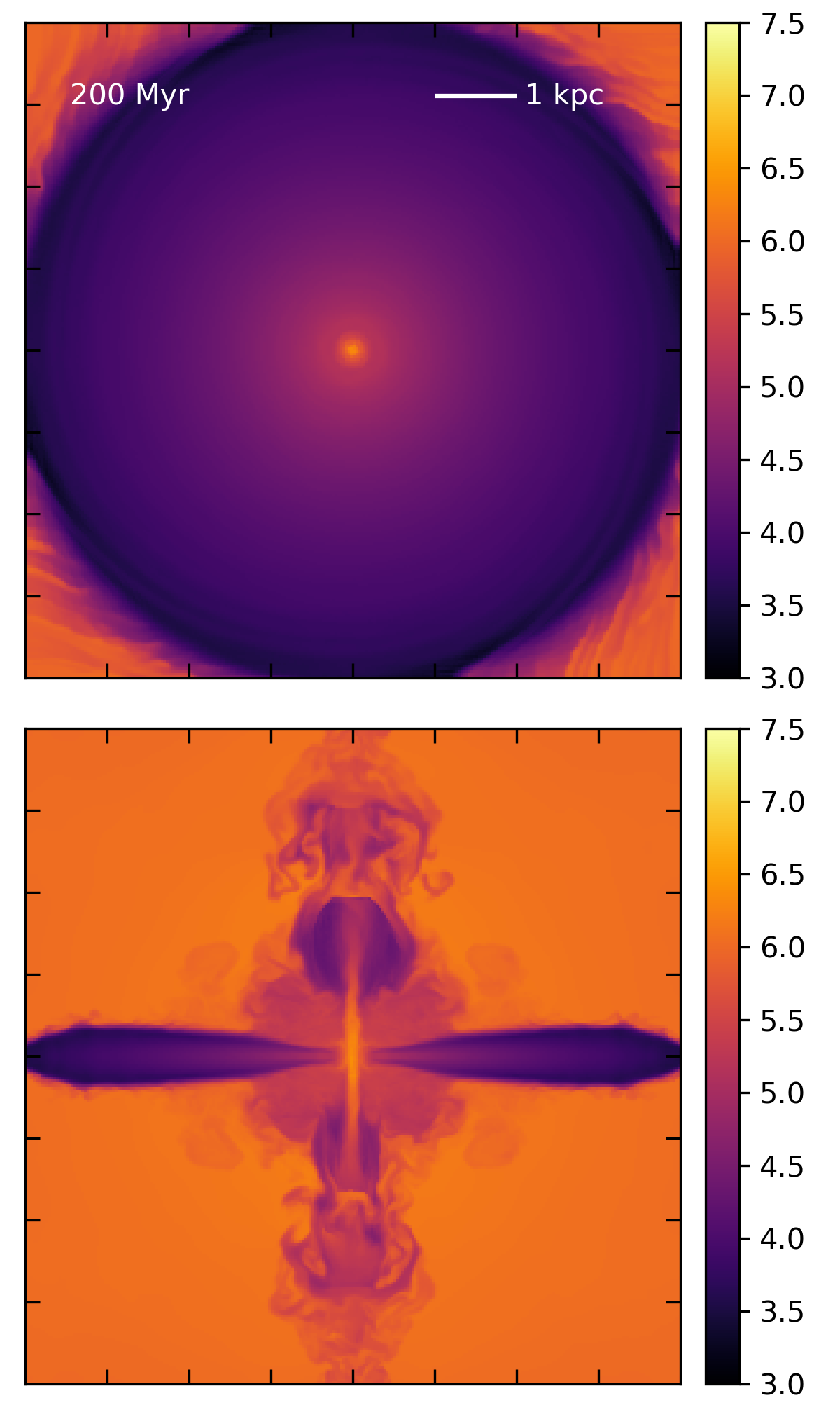 Resolution \(512^3\):
Resolution \(512^3\):
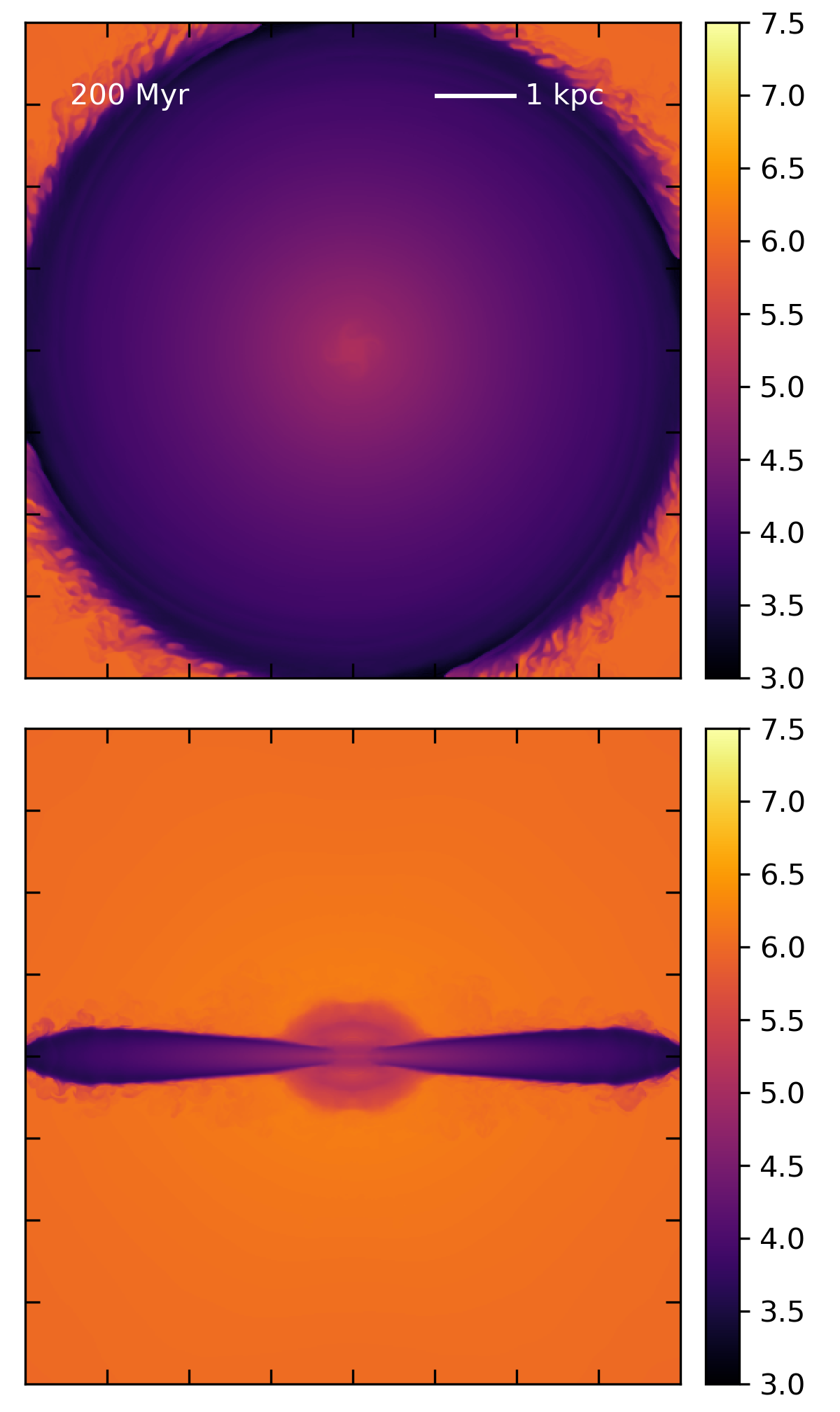
The central temperatures are obviously different, despite the fact that I’m dumping the same amount of mass and energy into an equal volume in each. (It’s also worth noting that for both of them, the central temperatures are well below what is predicted by the CC85 analytic solution, so it’s not surprising that I’m not getting outflowing gas). I admit I’m puzzled by this behavior, but I’m trying to understand it as follows. Let’s say we have a volume of a certain size, V. Then let’s say we have two simulations of that volume, one with a single cell, and one with 8 cells (double the resolution). Now, we’ve specified that each volume has to contain the same amount of mass, so the average density must be the same. Now let’s consider what happens when we want to add a specific amount of energy to the volume. The total energy per unit time is constant, \(\dot{E}\). For the single cell simulation, I divide \(\dot{E}\) by the total volume, V, and multiply by the timestep, dt, and now I have the energy density I need to add to the total energy in the cell. For the 8 cell volume, I first divide \(\dot{E}\) by the number of cells over which I’m distributing the energy, then divide by the total volume, V, to convert to energy density. Given that the average density of the cells in the 8 cell volume is the same as the single cell, and temperature just goes as E/n, this will obviously result in a temperature that is lower by a factor of 8 in the multi-cell volume.
EDIT: Obviously, I was making a mistake. The problem was that for the multi-cell volume, I was dividing by the total volume, V, after I had already converted to the total energy that goes in a single cell. Instead, I should have divided each cell by its own volume to get energy density. In fact, this was what I was doing when I first wrote the code, but it resulted in such large energy additions that it caused the code to break immediately, and I assumed I was doing something wrong. Now I’m trying a corrected version where I add the right amount of mass and energy, but after 10 Myr of evolution, to see if that helps.