HLLC solver
March 2, 2016
I wrote a new HLLC Riemann solver for Cholla. It is based on Toro’s extension to the HLL solver that incoporates a contact wave (so there are two intermediate states, instead of just one), and uses estimates for the signal speeds described in Batten 1997. Advantages of this solver include the fact that it does not require an iterative scheme to calculate the pressure (so is less computationally expensive than the exact solver), it is positive definite (unlike a linearized solver), and it is generally less complicated than the Roe solver. Claims in the literature indicate that it is also highly robust and produces results that are competitive with an exact solver.
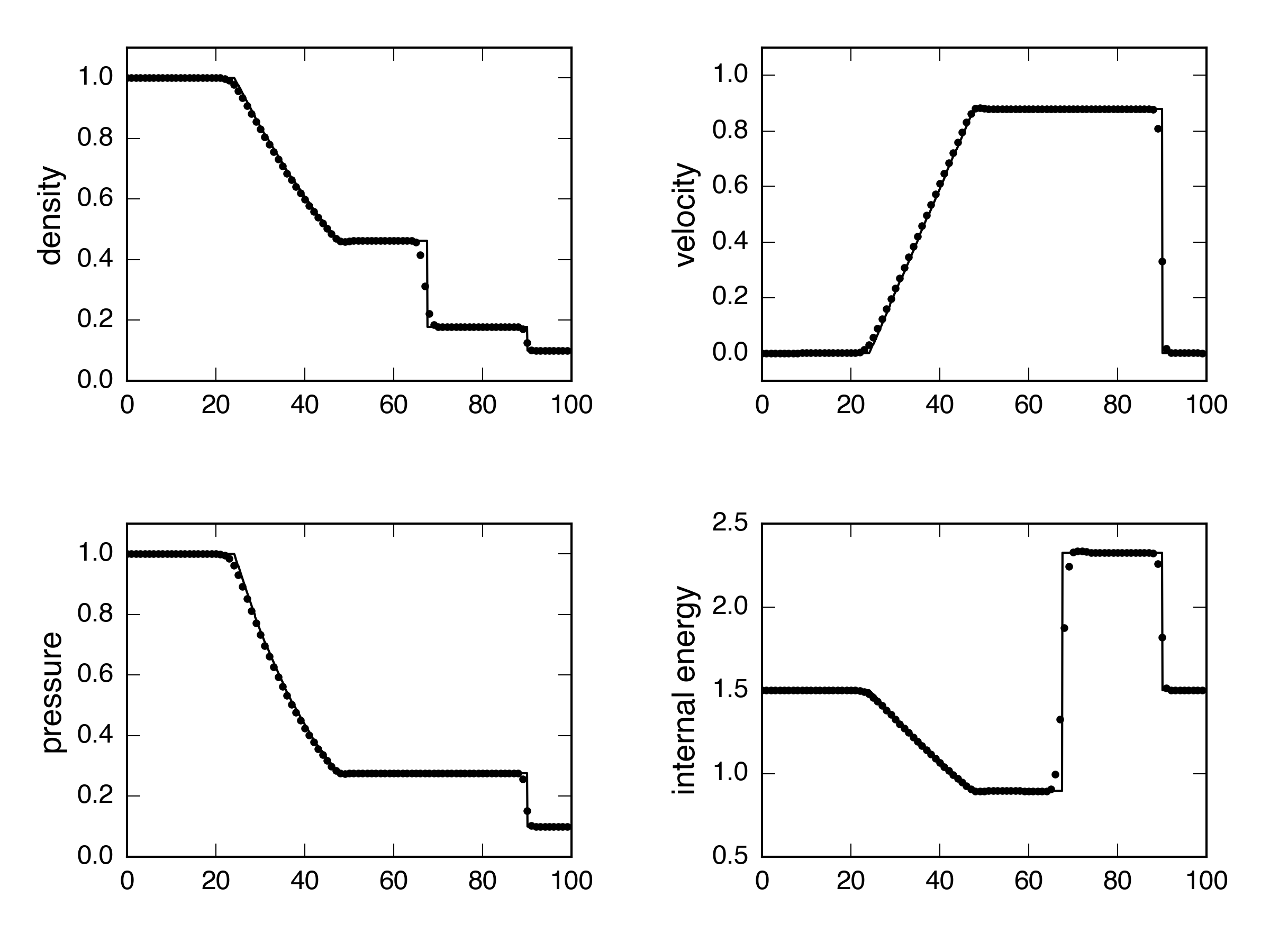
So, let’s look at some tests. First the standard Sod shock tube, using PPMC.
Exact:
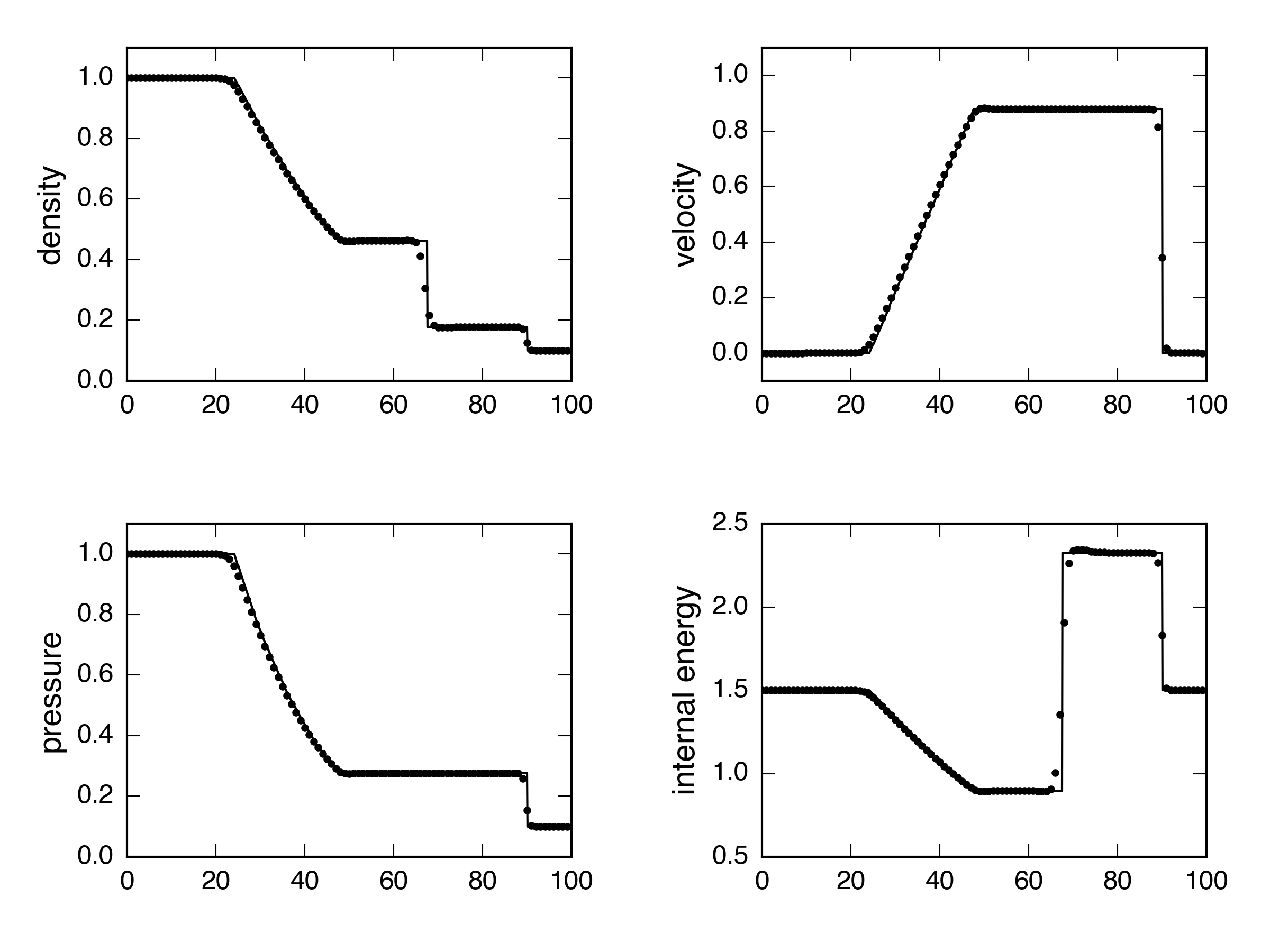
 HLLC:
HLLC:
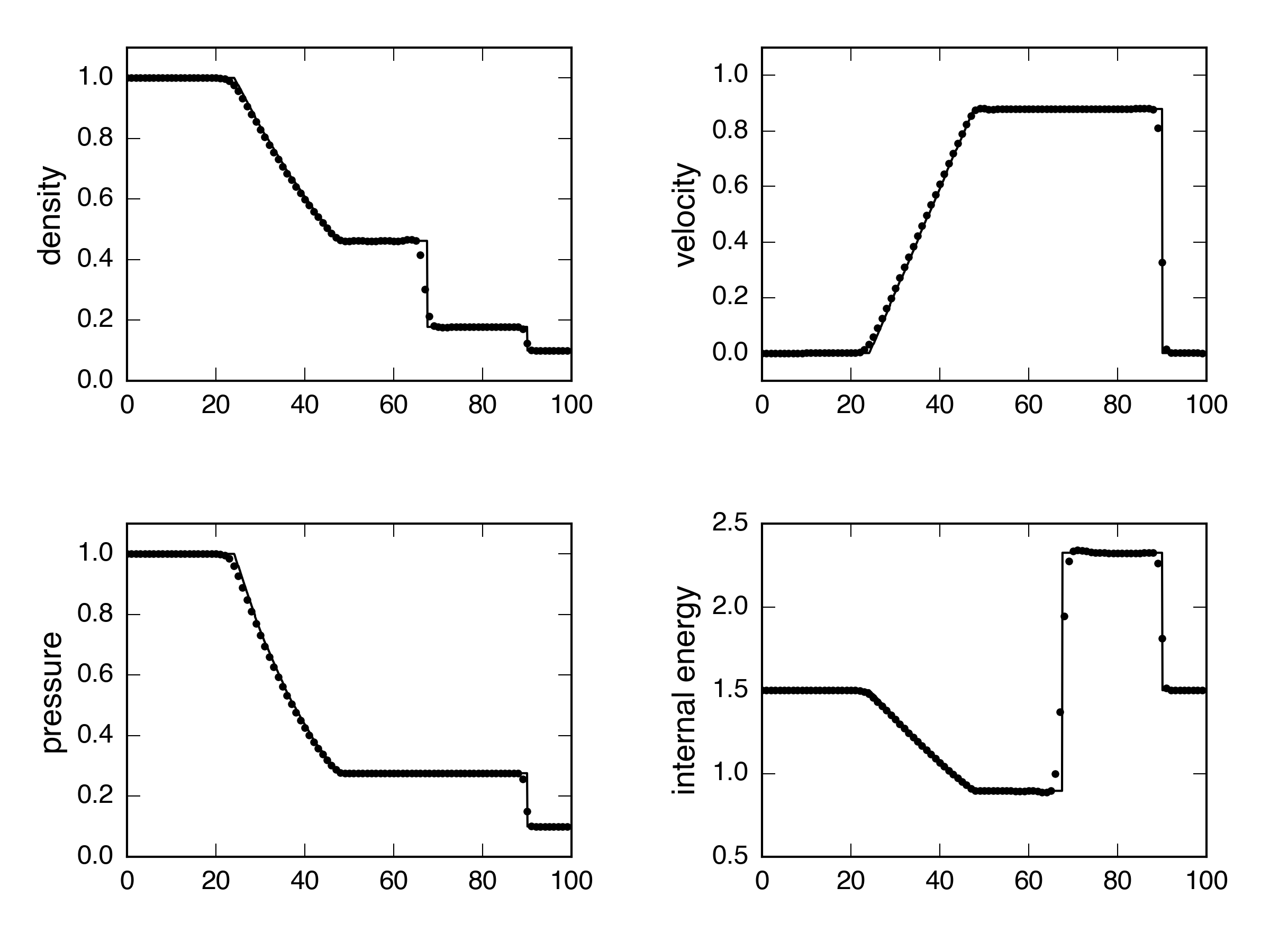
 Roe:
Roe:
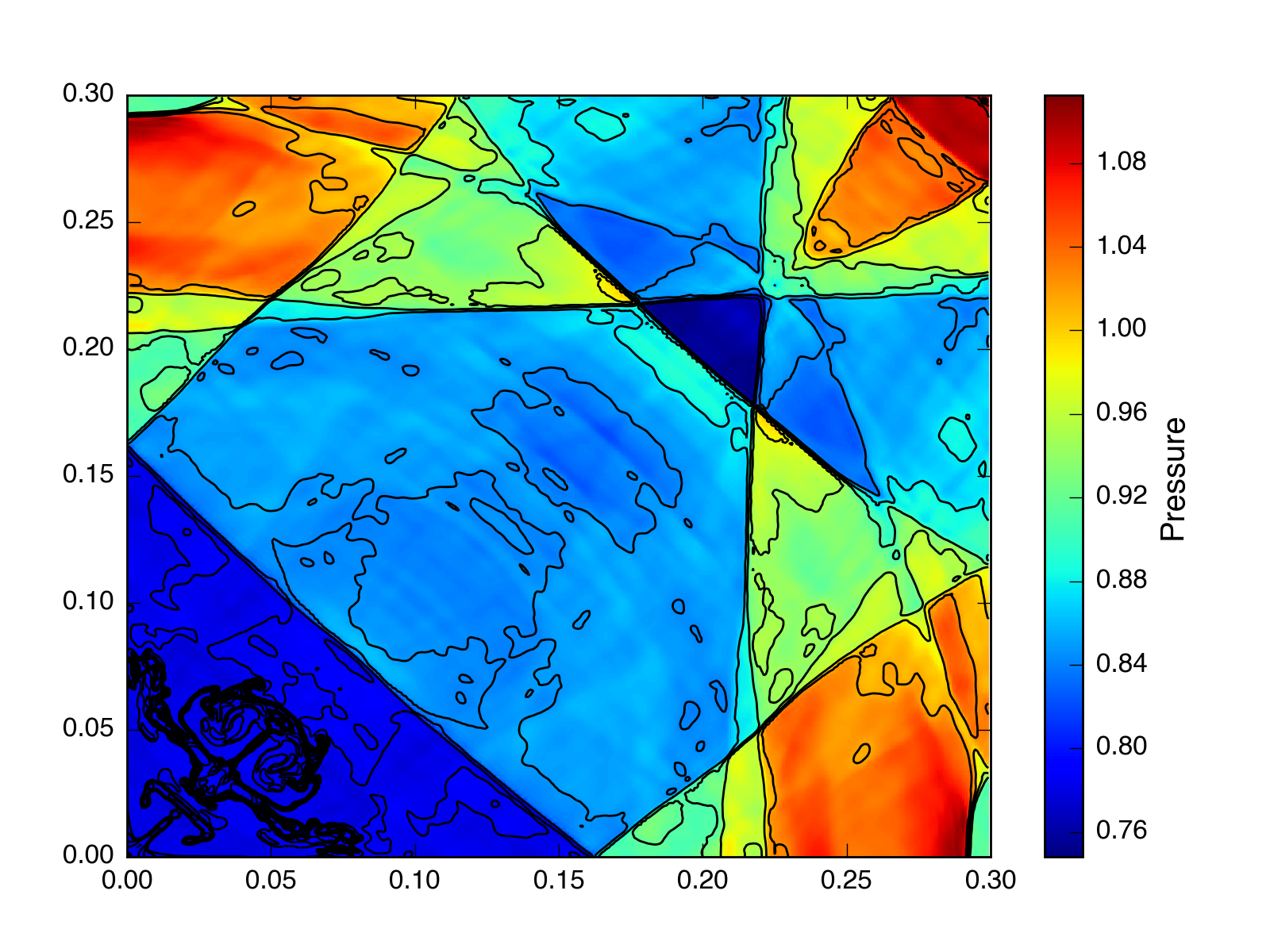
How about a strong shock?
Exact:
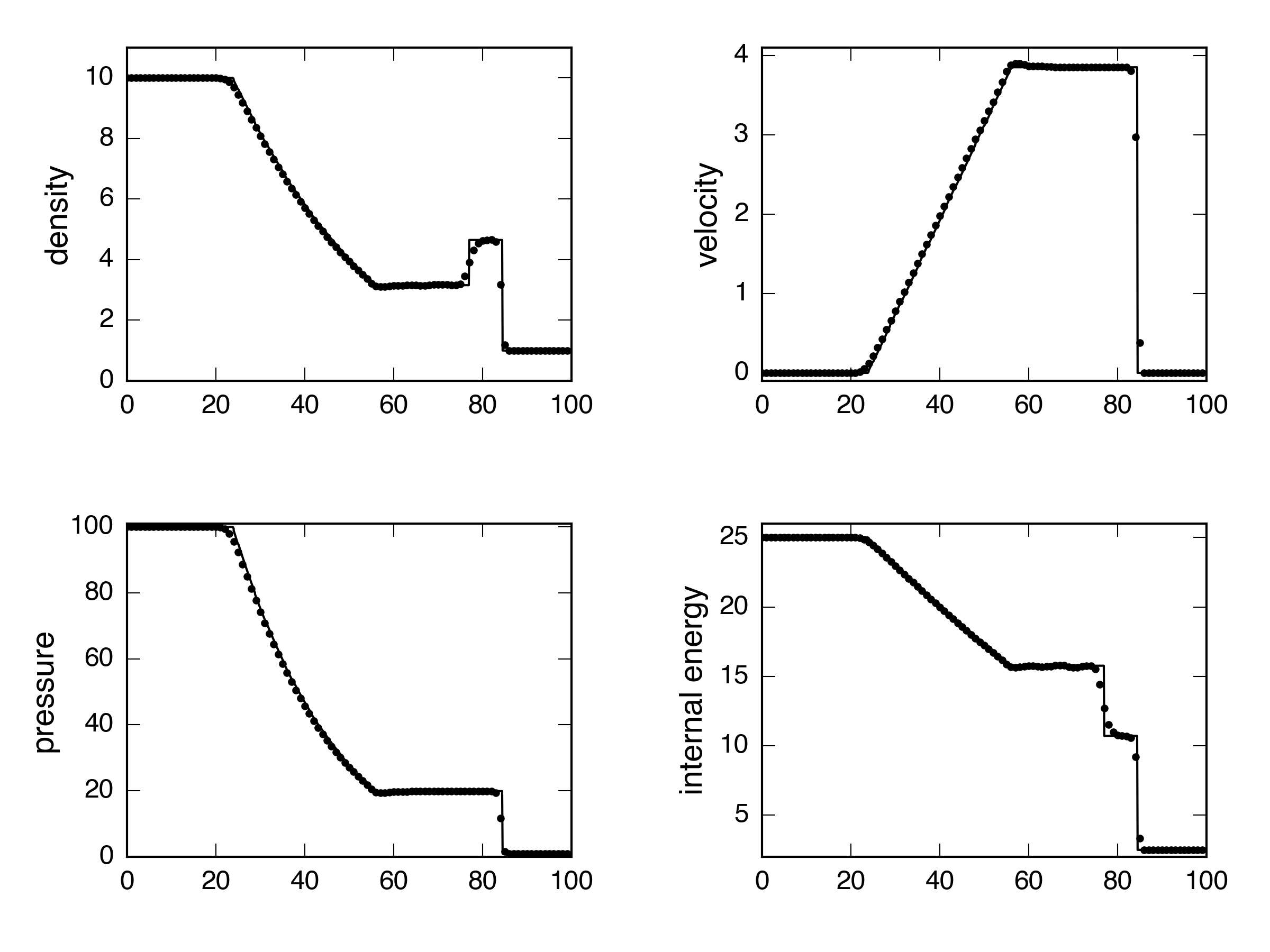 HLLC:
HLLC:
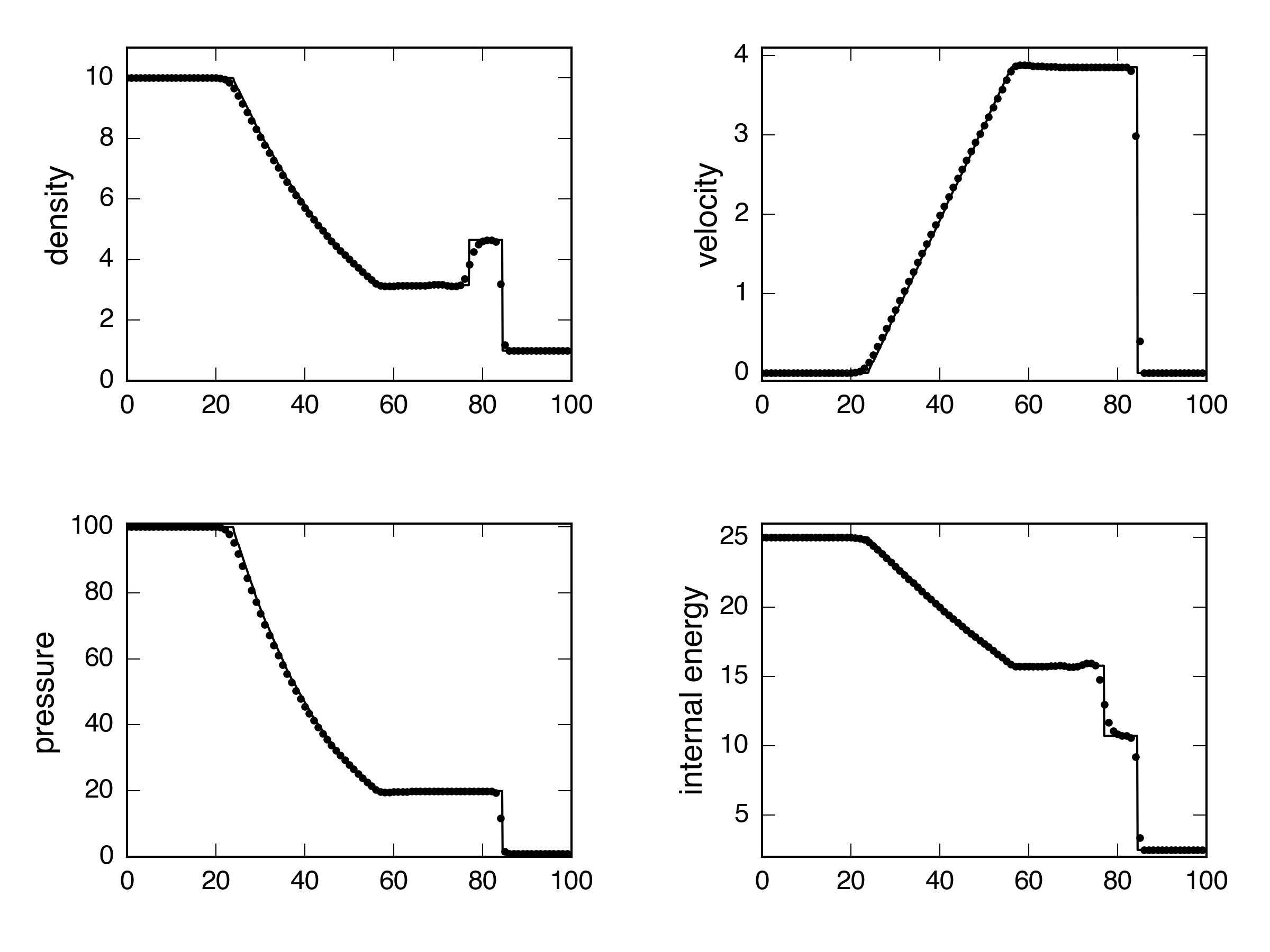 Roe:
Roe:
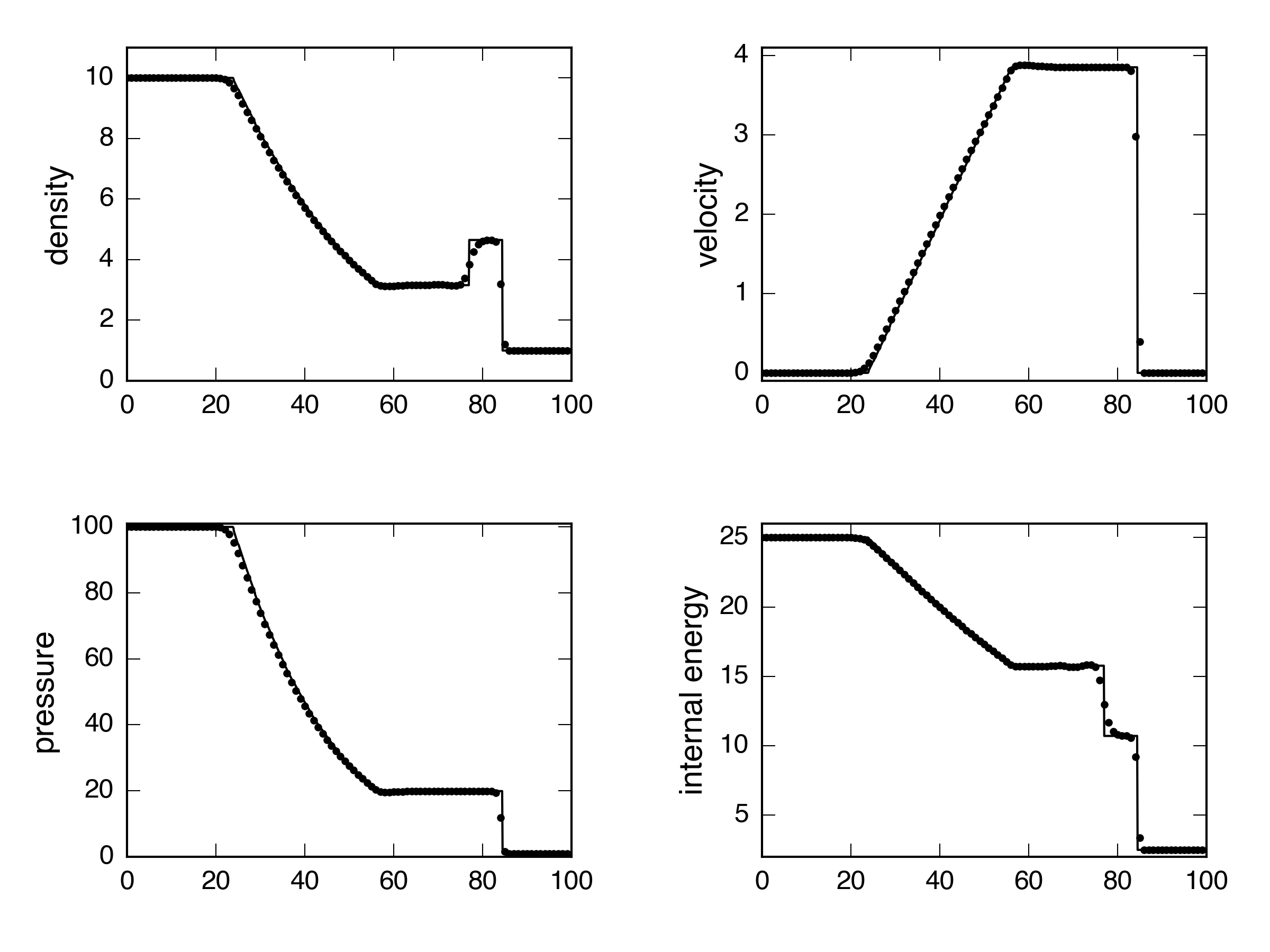
Maybe a little worse on the internal energy, but I’d say they all handle that one okay, as well. Now let’s try a \(400\times400\) implosion test. Again using PPMC, also with and without CTU.
Exact, \(t = 0.045\), without CTU (but with a CFL number = 0.1):
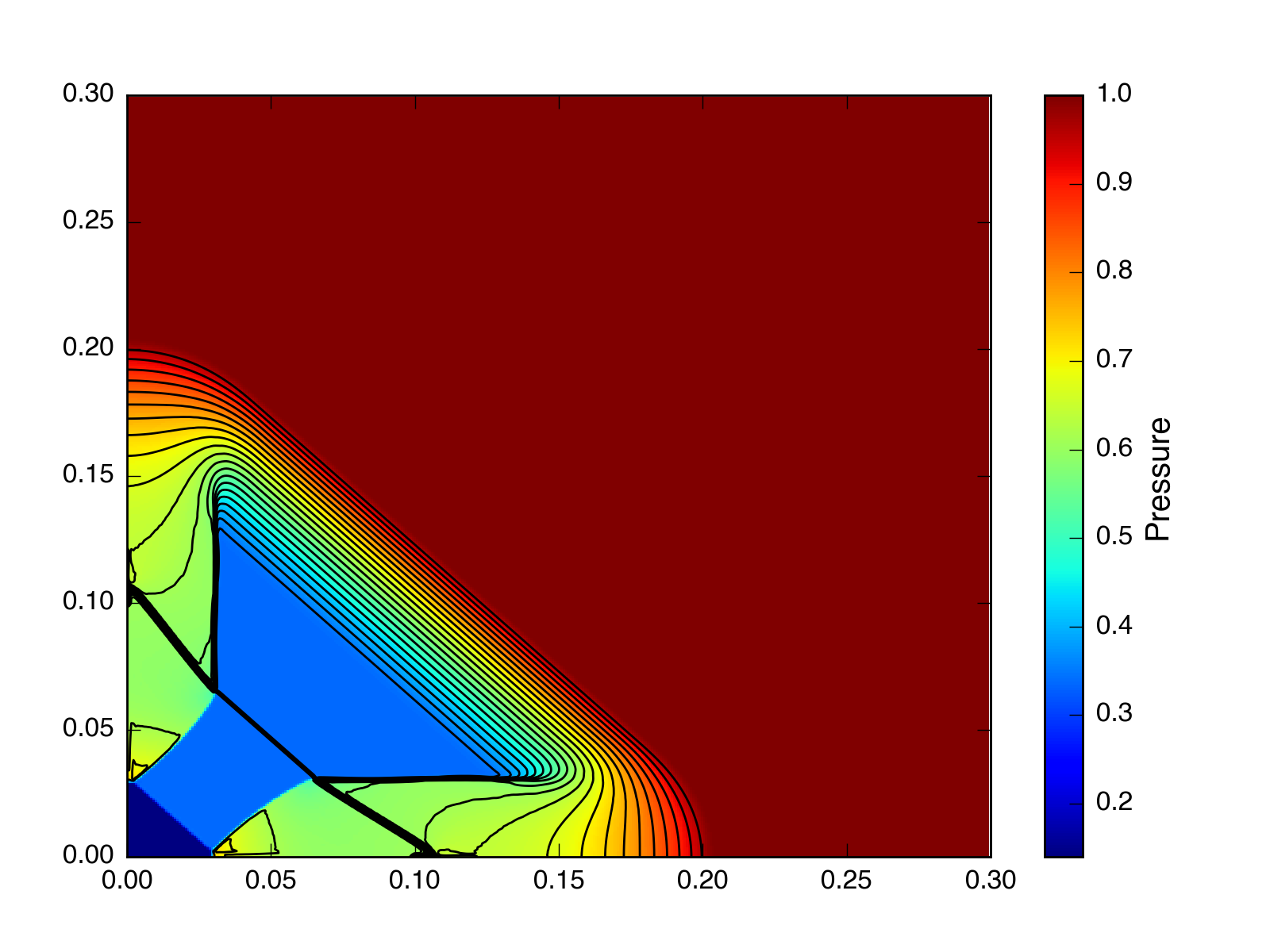
HLLC, \(t = 0.045\), without CTU (but with a CFL number = 0.1):
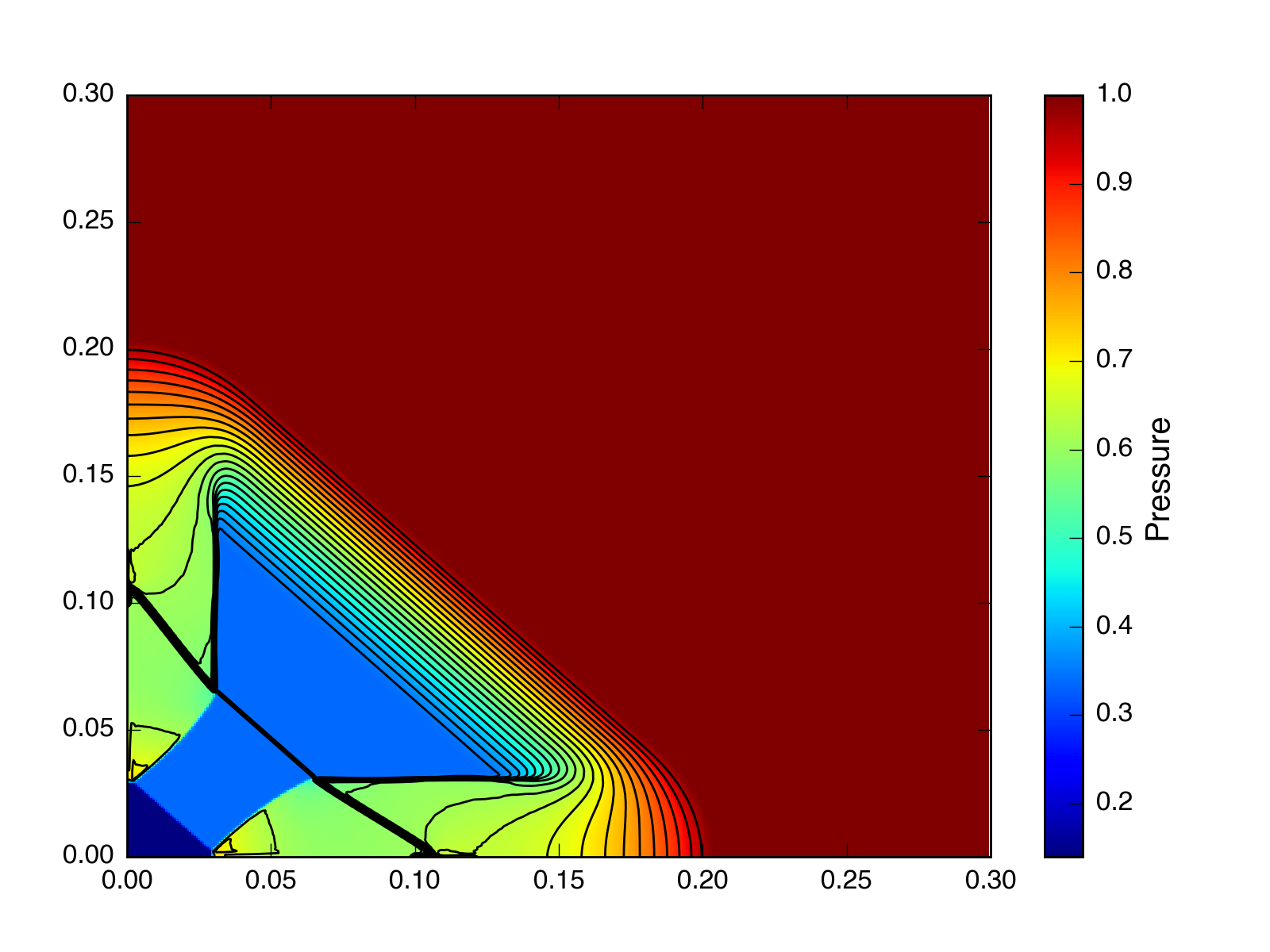
Roe, \(t = 0.045\), without CTU (but with a CFL number = 0.1):
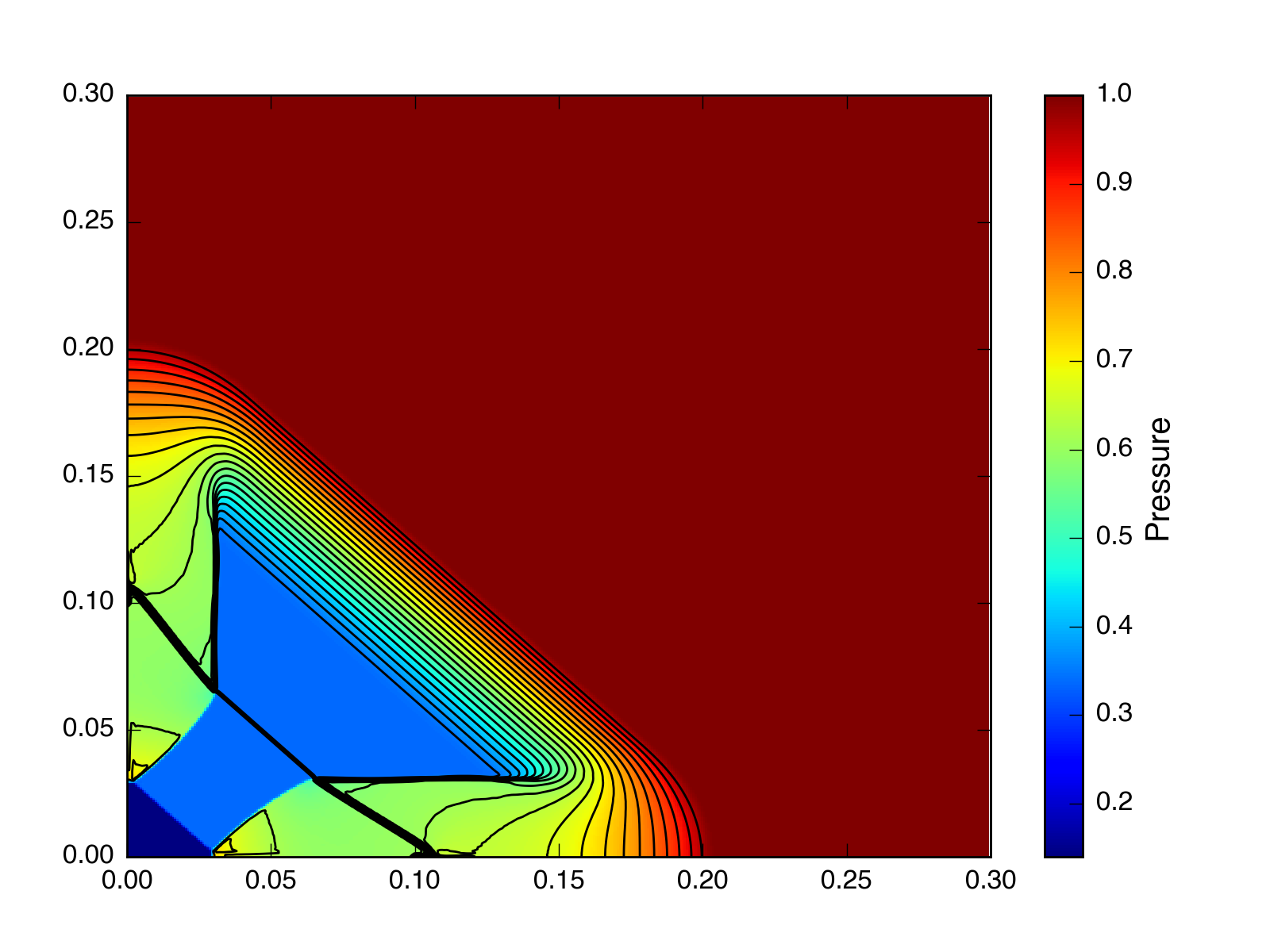
Exact, \(t = 2.5\), without CTU (but with a CFL number = 0.1):
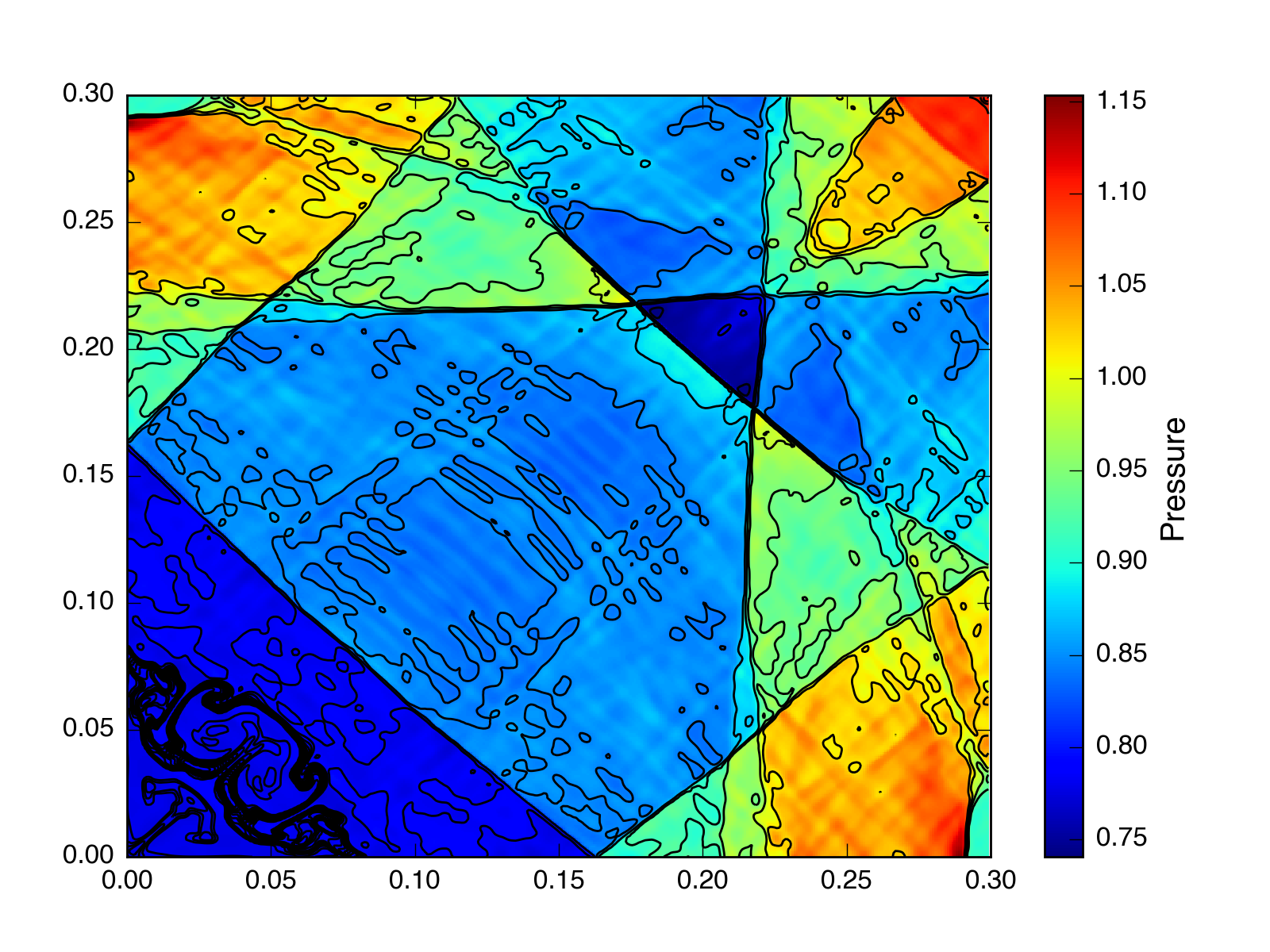
HLLC, \(t = 2.5\), without CTU (but with a CFL number = 0.1):
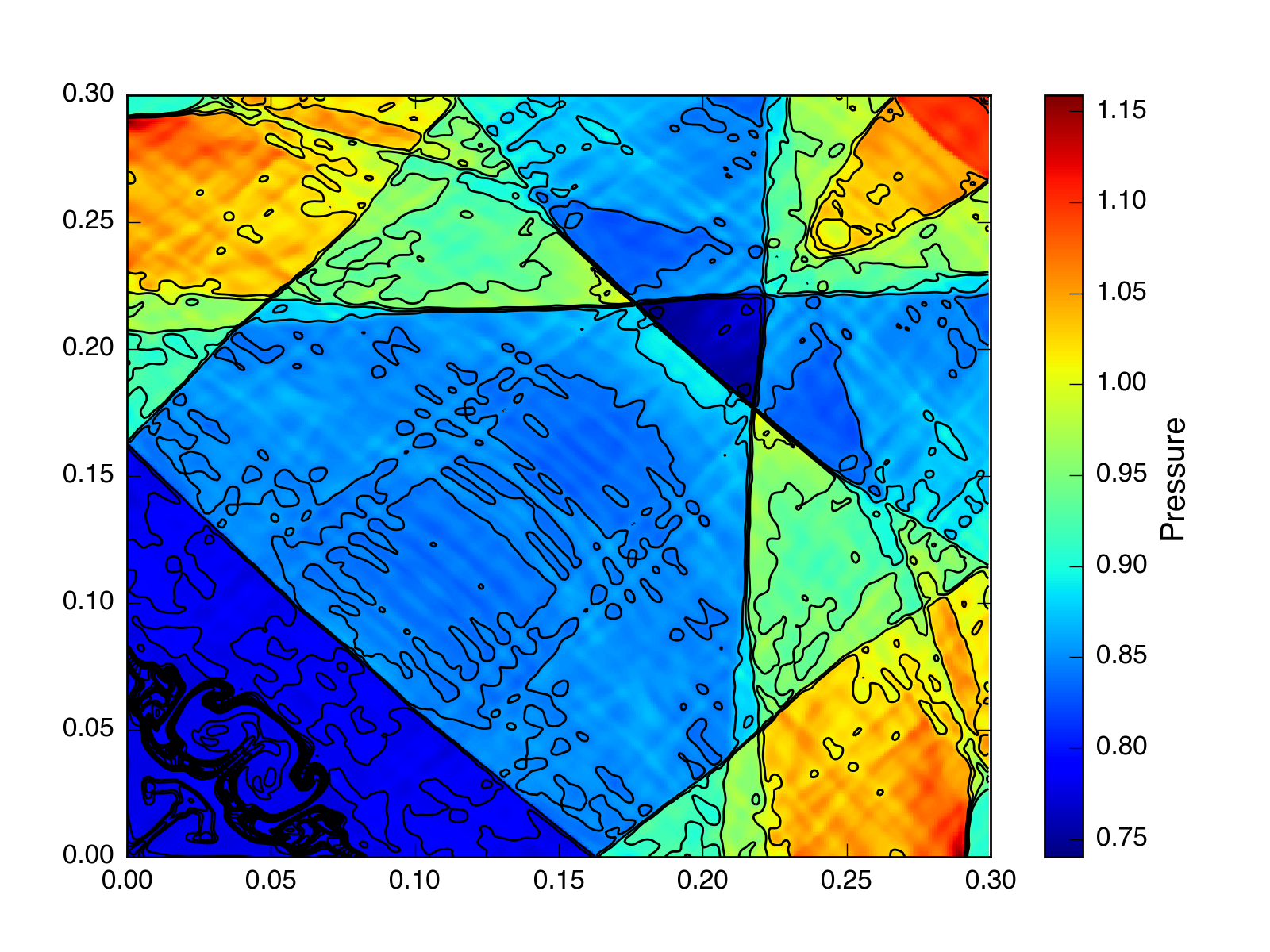
Roe, \(t = 2.5\), without CTU (but with a CFL number = 0.1):

The results look strikingly similar.
Here’s the same implosion test at \(t = 2.5\) with HLLC, CTU, and a CFL number = 0.4:
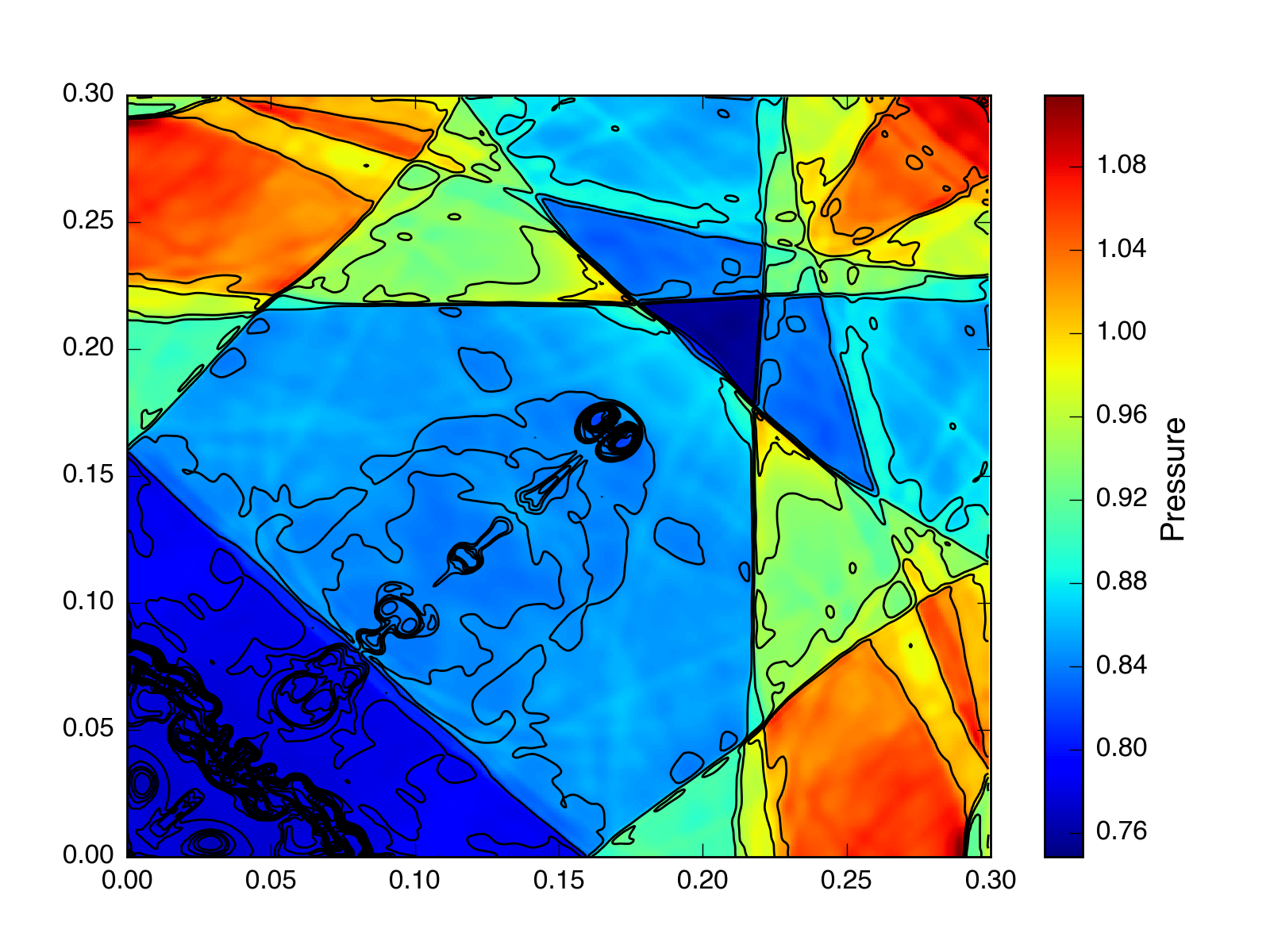
And at \(t = 2.5\) with HLLC, VL, and a CFL number = 0.4:
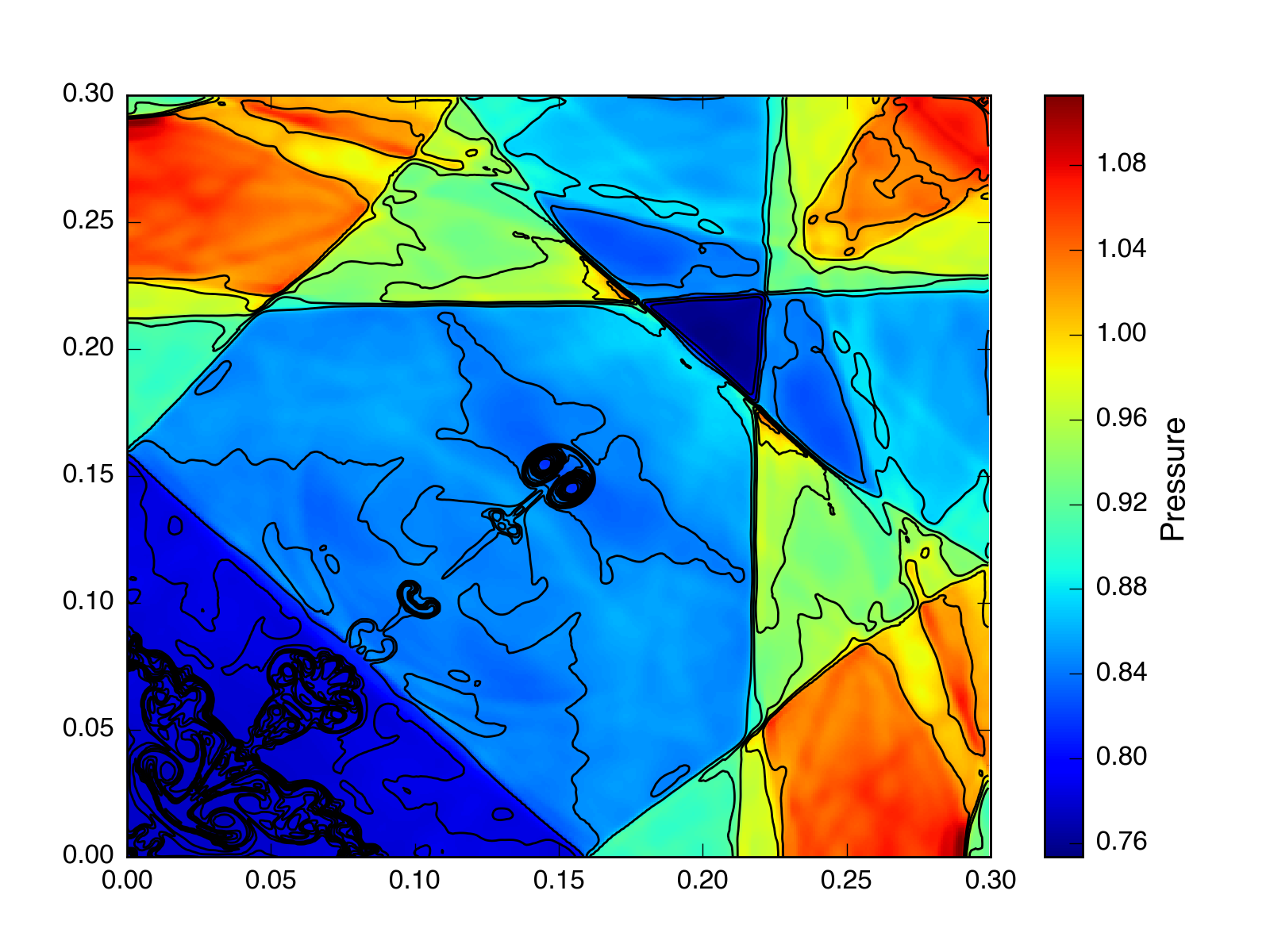
Interestingly, all these tests look better at late times than the PPMP test from the last post, even without CTU. Additionaly, the VL test looks more symmetric, although it is still not exactly symmetric like CTU. I’m looking into whether the problem in the last test was PPMP or the cfl number (0.25 vs 0.1). It doesn’t seem to be related to the Riemann solver.
UPDATE: It looks like the problem was the CFL number.
At \(t = 2.5\) with PPMP, HLLC, and no CTU (but with a CFL number 0.1):