Gresho Test

December 19, 2016

The Gresho vortex test is a notoriously difficult problem for grid-based (and SPH) codes. A rotating vortex is initialized such that the centrifugal force is balanced by the pressure gradient. The solution is time-independent. For these tests, I used the initial conditions described in Liska & Wendroff (2003).

Definitions

The velocity in the gresho problem is specified in polar coordinates, which I convert to Cartesian to initialize the voretx. Given

$$x = r \mathrm{cos}(\phi) \quad \mathrm{and} \quad y = r \mathrm{sin}(\phi),$$

I get

$$v_{x} = v_{r}\mathrm{cos}\phi - v_{\phi} \mathrm{sin}(\phi) \quad \mathrm{and} \quad v_{y} = v_{r}\mathrm{sin}(\phi) + v_{\phi}\mathrm{cos}(\phi)$$

(where $v_{\phi} = r \frac{d(\phi)}{dt}$). Since $v_{r} = 0$ for the Gresho problem, that gives

$$v_{x} = -v_{\phi}\mathrm{sin}(\phi) \quad \mathrm{and} \quad v_{y} = v_{\phi}\mathrm{cos}(\phi).$$

$\phi$ is calculated from $x$ and $y$ using $\phi= \mathrm{arctan}(\frac{y}{x})$ and $r$ using $r^2 = x^2 + y^2$.

In plotting the data, the conversion goes the other direction, from $v_{x}, v_{y}$ to $v_{\phi}$. After a similar derivative analysis, I get

$$v_{\phi} = \sqrt{x^2 + y^2} \frac{x v_y - y v_x}{x^2 + y^2}.$$

How about the vorticity? Vorticity is the curl of the velocity field, so in 2D it’s

$$\omega = \nabla \times v = \left(\frac{\delta(v_y)}{\delta x} - \frac{\delta(v_x)}{\delta y}\right)\hat{z},$$

or in polar coordinates

$$\omega = \nabla \times v = \frac{1}{r}\left(\frac{\delta(r v_\phi)}{\delta r} - \frac{\delta(v_r)}{\delta\phi}\right)\hat{z}.$$

Results

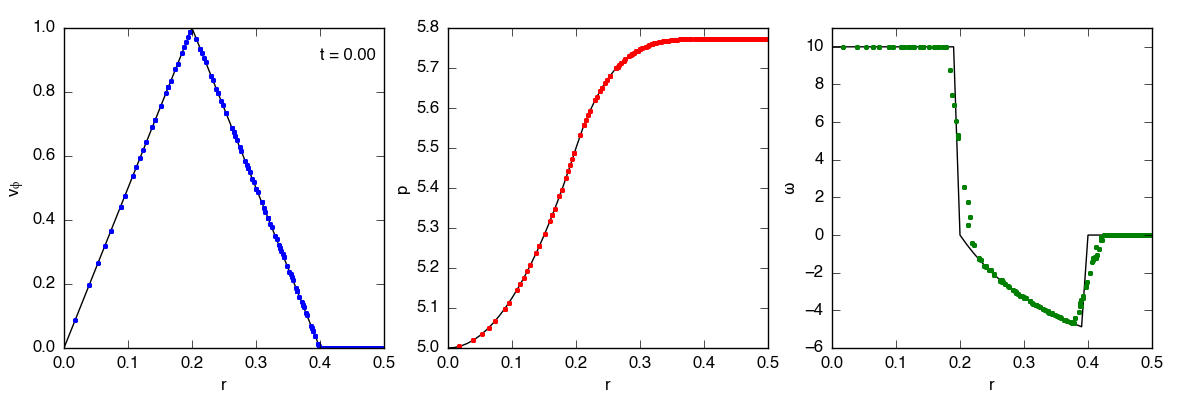
I’m running the test until t = 3.0 on a 40x40 grid with transmissive boundaries, PPMC, the exact solver, and CTU. The domain is x = [0, 1], y = [0, 1], with the vortex centered at (x, y) = (0.5, 0.5). The movies below show the evolution in azimuthal velocity ($v_\phi$), pressure, and vorticity ($\omega$). For $v_\phi$ and $p$, both 1D and 2D projections are shown.

L1 error

The L1 error is a useful measurement of how well the code is doing, as well as the convergence rate for this test. I calculate the L1 error for vorticity and density using the standard definition

$$\delta\mathbf{q} = \frac{1}{N}\sum|\mathbf{q}_i - \mathbf{q}_i^0|,$$

where $\mathbf{q}_i^0$ is the initial solution, and $N$ is the total number of points. The L1 errors for density and vorticity are 0.14% and 135% on a $20\times20$ grid, and 0.04% and 80% on a $40\times40$ grid.