Dual Energy Tests (Part 1)
September 29, 2015
Internal energy equations
From Teyssier 2015, the nonconservative internal energy update (Equation 161):
\[\frac{e^{n+1}_{\mathrm{prim}} - e^n}{\Delta t} = - \nabla \cdot \mathbf{F}(e)^n - P^n \nabla \cdot \mathbf{u}^n\]From Bryan et al. 2014, the nonconservative internal energy update (Equation 43):
\[\rho^{n+1}_j e^{n+1}_j = \rho^n_j e^n_j + \frac{\Delta t}{\Delta x_j} (\bar{\rho}_{j + \frac{1}{2}} \bar{v}_{j + \frac{1}{2}} \bar{e}_{j + \frac{1}{2}} - \bar{\rho}_{j - \frac{1}{2}} \bar{v}_{j - \frac{1}{2}} \bar{e}_{j - \frac{1}{2}}) - \frac{\Delta t}{\Delta x_j} p^n_j (\bar{v}_{j + \frac{1}{2}} - \bar{v}_{j - \frac{1}{2}})\]The switch
We need to decide when to use the nonconservative internal energy update, instead of the conservatively calculated internal energy, \(e_{\mathrm{int}} = e_T - 0.5\mathbf{v}\cdot\mathbf{v}.\)
Note: in Cholla notation, \(E = \rho e_T\), so \(e_{\mathrm{int}} = \frac{p}{\rho (\gamma - 1.0)}\). Cholla tracks \(E\) and \(\rho e_{\mathrm{int}}\).
In Teyssier 2015, the switch is calculated using an estimate for the truncation error of the method.
In Bryan 2014, the switch is made according to the ratio of internal energy to total energy.
The tests
The tests shown below consist of a shock tube with periodic boundaries, to allow for high mach number bulk flow.
\[\rho_L = 1.0,\quad v_L = 0.0,\quad p_L = 1.0 \\ \rho_R = 0.2,\quad v_R = 0.0,\quad p_R = 0.01 \\ \gamma = 1.4\]For the high mach number test, \(v_L = v_R = 120\).
Without Dual Energy
Figure 1: PPMP, exact Riemann solver, CTU
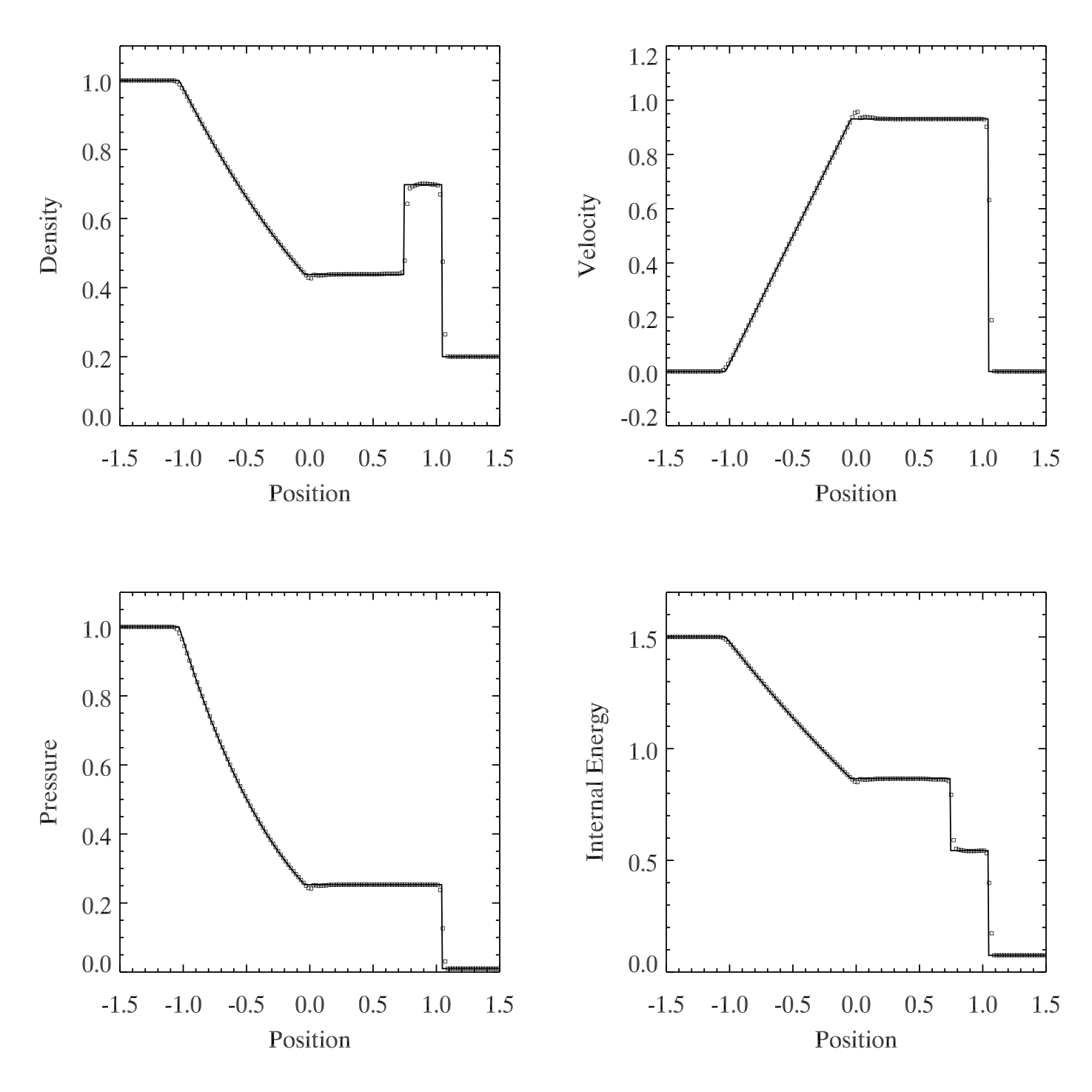
Figure 2: same as Figure 1, but with bulk velocity \(v_{bulk} = 100 c_s\)
